–ë–Α–Ϋ–Ϋ–Β―Ä

–£–Η–±―Ä–Ψ–Η―¹―²–Ψ―΅–Ϋ–Η–Κ –Ϋ–Α –≥―É―¹–Β–Ϋ–Η―΅–Ϋ―΄―Ö ―²–Β–Μ–Β–Ε–Κ–Α―Ö
|
¬ß 50. –ü–Ψ–Μ―è―Ä–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –Η –Β–≥–Ψ ―Ä–Β―à–Β–Ϋ–Η–Β
–ü–Ψ–Μ―è―Ä–Ϋ―΄–Φ (–Η–Μ–Η –Ω–Α―Ä–Α–Μ–Μ–Α–Κ―²–Η―΅–Β―¹–Κ–Η–Φ) ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–Φ –Ϋ–Α–Ζ―΄–≤–Α―é―²
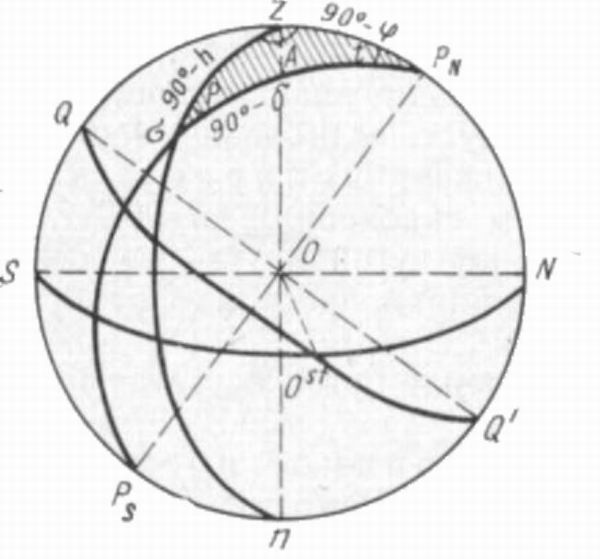
―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Η–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –Ϋ–Α –Ϋ–Β–±–Β―¹–Ϋ–Ψ–Ι ―¹―³–Β―Ä–Β, –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ―΄–Ι –≤ ―Ä–Β–Ζ―É–Μ―¨―²–Α―²–Β –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è ―²―Ä–Β―Ö –¥―É–≥ –±–Ψ–Μ―¨―à–Η―Ö –Κ―Ä―É–≥–Ψ–≤: –Φ–Β―Ä–Η–¥–Η–Α–Ϋ–Α –Ϋ–Α–±–Μ―é–¥–Α―²–Β–Μ―è, –Κ―Ä―É–≥–Α ―¹–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η―è –Η –≤–Β―Ä―²–Η–Κ–Α–Μ–Α ―¹–≤–Β―²–Η–Μ–Α (―Ä–Η―¹. 75). –≠–Μ–Β–Φ–Β–Ϋ―²–Α–Φ–Η –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―è–≤–Μ―è―é―²―¹―è ―É–≥–Ψ–Μ ZP N a=t βÄî ―΅–Α―¹–Ψ–≤–Ψ–Ι ―É–≥–Ψ–Μ
(–≤ –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Ψ–Φ ―¹―΅–Β―²–Β); ―É–≥–Ψ–Μ –±ZP N = AβÄî–Α–Ζ–Η–Φ―É ―² (–≤ –Ω–Ψ–Μ―É–Κ―Ä―É–≥–Ψ–≤–Ψ–Φ
―¹―΅–Β―²–Β); ―É–≥–Ψ–Μ ZoPn = P βÄî –Ω–Α―Ä–Α–Μ–Μ–Α–Κ―²–Η―΅–Β―¹–Κ–Η–Ι ―É–≥–Ψ–Μ: ―¹―²–Ψ―Ä–Ψ–Ϋ–Α PNZ βÄî –¥–Ψ–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η–Β ―à–Η―Ä–Ψ―²―΄ –¥–Ψ 90¬Α, ―². –Β. (90¬ΑβÄîφ); ―¹―²–Ψ―Ä–Ψ–Ϋ–Α PNo βÄî –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β ―¹–≤–Β―²–Η–Μ–Α –ê = 90¬ΑβÄî–Ψ, ―¹―²–Ψ―Ä–Ψ–Ϋ–Α Zo βÄî –Ζ–Β–Ϋ–Η―²–Ϋ–Ψ–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β
z = 90¬ΑβÄîh.
–ü–Α―Ä–Α–Μ–Μ–Α–Κ―²–Η―΅–Β―¹–Κ–Η–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―¹–≤―è–Ζ―΄–≤–Α–Β―² –≥–Ψ―Ä–Η–Ζ–Ψ–Ϋ―²–Ϋ―΄–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ h –Η –ê, ―ç–Κ–≤–Α―²–Ψ―Ä–Η–Α–Μ―¨–Ϋ―΄–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ –≥ –Η –± –Η –≥–Β–Ψ–≥―Ä–Α―³–Η―΅–Β―¹–Κ–Η–Β
–Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ φ –Η λ –Φ–Β―¹―²–Α –Ϋ–Α–±–Μ―é–¥–Α―²–Β–Μ―è. –™–Β–Ψ–≥―Ä–Α―³–Η―΅–Β―¹–Κ–Α―è –¥–Ψ–Μ–≥–Ψ―²–Α –·,
–Κ–Α–Κ –±―É–¥–Β―² –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –¥–Α–Μ―¨―à–Β, –≤―Ö–Ψ–¥–Η―² –≤ ―΅–Α―¹–Ψ–≤–Ψ–Ι ―É–≥–Ψ–Μ t.
–≠―²–Ψ–Ι ―¹–≤―è–Ζ―¨―é –Ψ–±―ä―è―¹–Ϋ―è–Β―²―¹―è –±–Ψ–Μ―¨―à–Α―è –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Α―è ―Ü–Β–Ϋ–Ϋ–Ψ―¹―²―¨ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –ï―¹–Μ–Η –Η–Ζ–≤–Β―¹―²–Ϋ―΄ ―²―Ä–Η –Β–≥–Ψ ―ç–Μ–Β–Φ–Β–Ϋ―²–Α, ―²–Ψ –Φ–Ψ–Ε–Ϋ–Ψ,
―Ä–Β―à–Η–≤ –Β–≥–Ψ, –Ϋ–Α–Ι―²–Η –Ψ―¹―²–Α–Μ―¨–Ϋ―΄–Β –Ϋ–Β–Η–Ζ–≤–Β―¹―²–Ϋ―΄–Β ―ç–Μ–Β–Φ–Β–Ϋ―²―΄, –≤ ―΅–Α―¹―²–Ϋ–Ψ―¹―²–Η
–≥–Β–Ψ–≥―Ä–Α―³–Η―΅–Β―¹–Κ―É―é ―à–Η―Ä–Ψ―²―É –Η–Μ–Η –¥–Ψ–Μ–≥–Ψ―²―É.
–†–Β―à–Β–Ϋ–Η–Β –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–≥–Ψ ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –≤–Ψ–Ζ–Φ–Ψ–Ε–Ϋ–Ψ, –Β―¹–Μ–Η –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ –Ϋ–Β –Φ–Β–Ϋ–Β–Β ―²―Ä–Β―Ö –Β–≥–Ψ ―ç–Μ–Β–Φ–Β–Ϋ―²–Ψ–≤. –Γ–≤―è–Ζ―¨ –Φ–Β–Ε–¥―É ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η –Η
–†–Η―¹. 75.
–†–Η―¹. 76.
―É–≥–Μ–Α–Φ–Η –≤ ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –≤―΄―Ä–Α–Ε–Α–Β―²―¹―è ―΅–Β―²―΄―Ä―¨–Φ―è –Ψ―¹–Ϋ–Ψ–≤–Ϋ―΄–Φ–Η ―³–Ψ―Ä–Φ―É–Μ–Α–Φ–Η ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Ψ–Ι ―²―Ä–Η–≥–Ψ–Ϋ–Ψ–Φ–Β―²―Ä–Η–Η.
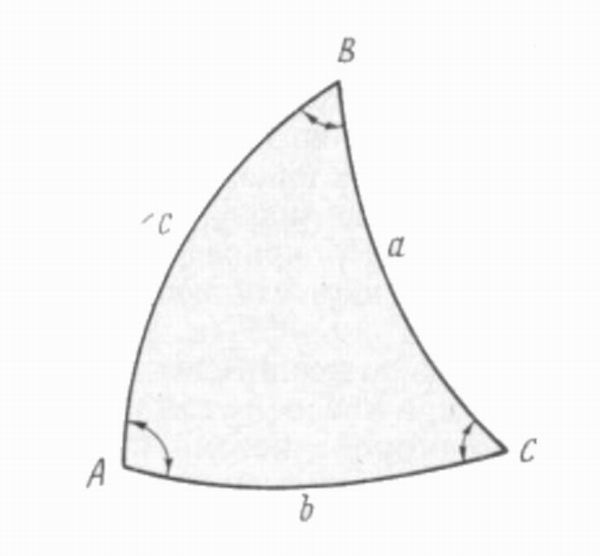
1. –Λ–Ψ―Ä–Φ―É–Μ–Α ―¹–Η–Ϋ―É―¹–Ψ–≤ (―Ä–Η―¹. 76). –£–Ψ –≤―¹―è–Κ–Ψ–Φ ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Ψ–Φ
―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ―¹–Η–Ϋ―É―¹―΄ ―¹―²–Ψ―Ä–Ψ–Ϋ –Ψ―²–Ϋ–Ψ―¹―è―²―¹―è –Κ–Α–Κ ―¹–Η–Ϋ―É―¹―΄ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄―Ö –Η–Φ ―É–≥–Μ–Ψ–≤:
ctg –ê = ctg –Α βÄΔ sin ―¹ βÄΔ cosec –£ βÄî cos ―¹ βÄΔ ctg –£ +I + II;
cos b = cos –Α βÄΔ cos ―¹ + sin –Α βÄΔ sin ―¹ βÄΔ cos B +I βÄî II;
2. –Λ–Ψ―Ä–Φ―É–Μ–Α –Κ–Ψ―¹–Η–Ϋ―É―¹–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄. –£–Ψ –≤―¹―è–Κ–Ψ–Φ ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –Κ–Ψ―¹–Η–Ϋ―É―¹ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Α–≤–Β–Ϋ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―é –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–≤
–¥–≤―É―Ö –¥―Ä―É–≥–Η―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ –Ω–Μ―é―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β ―¹–Η–Ϋ―É―¹–Ψ–≤ ―²–Β―Ö –Ε–Β ―¹―²–Ψ―Ä–Ψ–Ϋ, ―É–Φ–Ϋ–Ψ–Ε–Β–Ϋ–Ϋ–Ψ–Β –Ϋ–Α –Κ–Ψ―¹–Η–Ϋ―É―¹ ―É–≥–Μ–Α –Φ–Β–Ε–¥―É –Ϋ–Η–Φ–Η (―². –Β. –Ϋ–Α –Κ–Ψ―¹–Η–Ϋ―É―¹ ―É–≥–Μ–Α, –Ω―Ä–Ψ―²–Η–≤–Ψ–Μ–Β–Ε–Α―â–Β–≥–Ψ –Ω–Β―Ä–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Β).
3. –Λ–Ψ―Ä–Φ―É–Μ–Α –Κ–Ψ―¹–Η–Ϋ―É―¹–Α ―É–≥–Μ–Α. –ö–Ψ―¹–Η–Ϋ―É―¹ ―É–≥–Μ–Α ―Ä–Α–≤–Β–Ϋ –Φ–Η–Ϋ―É―¹
–Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―é –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–≤ –¥–≤―É―Ö –¥―Ä―É–≥–Η―Ö ―É–≥–Μ–Ψ–≤ –Ω–Μ―é―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β
―¹–Η–Ϋ―É―¹–Ψ–≤ ―²–Β―Ö –Ε–Β ―É–≥–Μ–Ψ–≤ –Ϋ–Α –Κ–Ψ―¹–Η–Ϋ―É―¹ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄, –Μ–Β–Ε–Α―â–Β–Ι –Φ–Β–Ε–¥―É –Ϋ–Η–Φ–Η
(―². –Β. –Ω―Ä–Ψ―²–Η–≤–Ψ–Μ–Β–Ε–Α―â–Β–Ι –Ω–Β―Ä–≤–Ψ–Φ―É ―É–≥–Μ―É).
4. –Λ–Ψ―Ä–Φ―É–Μ–Α –Κ–Ψ―²–Α–Ϋ–≥–Β–Ϋ―¹–Ψ–≤. –£–Ψ –≤―¹―è–Κ–Ψ–Φ ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Κ–Ψ―²–Α–Ϋ–≥–Β–Ϋ―¹–Α –Κ―Ä–Α–Ι–Ϋ–Β–≥–Ψ ―É–≥–Μ–Α –Ϋ–Α ―¹–Η–Ϋ―É―¹ ―¹―Ä–Β–¥–Ϋ–Β–≥–Ψ ―É–≥–Μ–Α ―Ä–Α–≤–Ϋ–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―é –Κ–Ψ―²–Α–Ϋ–≥–Β–Ϋ―¹–Α –Κ―Ä–Α–Ι–Ϋ–Β–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Ϋ–Α ―¹–Η–Ϋ―É―¹ ―¹―Ä–Β–¥–Ϋ–Β–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Φ–Η–Ϋ―É―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–≤ ―¹―Ä–Β–¥–Ϋ–Η―Ö ―ç–Μ–Β–Φ–Β–Ϋ―²–Ψ–≤.
–ü―Ä–Α–≤―΄–Β ―΅–Α―¹―²–Η ―³–Ψ―Ä–Φ―É–Μ (61) βÄî (63) –Ϋ–Β–Μ–Ψ–≥–Α―Ä–Η―³–Φ–Η―΅–Β―¹–Κ–Η–Β –Η –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è―é―² ―¹–Ψ–±–Ψ–Ι ―¹―É–Φ–Φ―É –Η–Μ–Η ―Ä–Α–Ζ–Ϋ–Ψ―¹―²―¨ –¥–≤―É―Ö ―΅–Μ–Β–Ϋ–Ψ–≤. –ü–Ψ―ç―²–Ψ–Φ―É –Ω―Ä–Η
―Ä–Β―à–Β–Ϋ–Η–Η –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨―¹―è –≤―¹–Ω–Ψ–Φ–Ψ–≥–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―²–Α–±–Μ–Η―Ü–Α–Φ–Η
–¥–Μ―è ―¹―É–Φ–Φ –Η ―Ä–Α–Ζ–Ϋ–Ψ―¹―²–Β–Ι –Μ–Ψ–≥–Α―Ä–Η―³–Φ–Ψ–≤ (―²–Α–±–Μ–Η―Ü―΄ –™–Α―É―¹―¹–Α), –Ω–Ψ–Φ–Β―â–Β–Ϋ–Ϋ―΄–Φ–Η –≤ –€–Δ-63.
–ü―Ä–Η–Φ–Β―Ä 33. –î–Α–Ϋ–Ψ: –Α = 67¬Α19',6, ―¹=33¬Α42',8 , –£ = 118¬Α00',9. –ù–Α–Ι―²–Η –ê, b, –Γ.
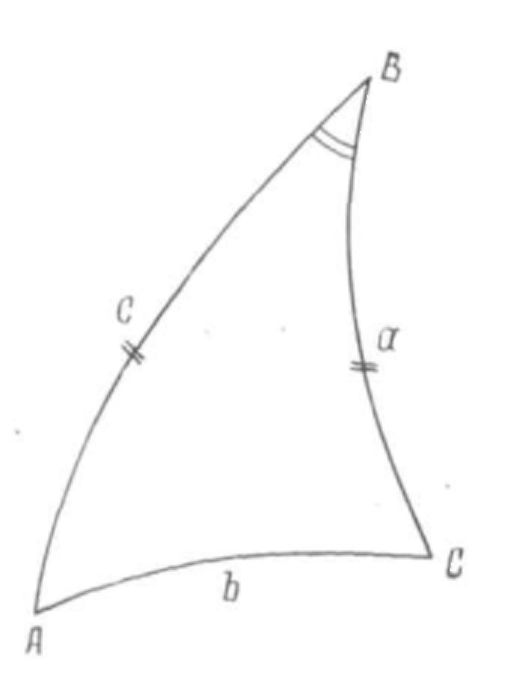
–†–Β―à–Β–Ϋ–Η–Β. 1. –ü–Ψ–Μ―¨–Ζ―É―è―¹―¨ ―¹―³–Β―Ä–Η―΅–Β―¹–Κ–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–Φ, –≤―΄–Ω–Η―¹―΄–≤–Α–Β–Φ ―³–Ψ―Ä–Φ―É–Μ―΄,
―¹–≤―è–Ζ―΄–≤–Α―é―â–Η–Β ―²―Ä–Η –Η–Ζ–≤–Β―¹―²–Ϋ―΄―Ö ―ç–Μ–Β–Φ–Β–Ϋ―²–Α ―¹ –Η―¹–Κ–Ψ–Φ―΄–Φ (―Ä–Η―¹. 77).
ctg –ê βÄΔ sin –£ = ctg –Α βÄΔ sin ―¹ βÄî cos ―¹ βÄΔ cos –£;
cos b = cos –Α βÄΔ cos ―¹ + sin –Α βÄΔ sin ―¹ βÄΔ cos –£;
ctg –Γ βÄΔ sin –£ = ctg ―¹ βÄΔ sin –Α βÄî cos a βÄΔ cos –£.
2. –£ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ―΄―Ö ―³–Ψ―Ä–Φ―É–Μ–Α―Ö ―¹–Μ–Β–≤–Α –Ψ―¹―²–Α–≤–Μ―è–Β–Φ ―²–Ψ–Μ―¨–Κ–Ψ –Ϋ–Β–Η–Ζ–≤–Β―¹―²–Ϋ―΄–Β ―ç–Μ–Β–Φ–Β–Ϋ―²―΄.
–ê–Ϋ–Α–Μ–Η–Ζ–Η―Ä―É–Β–Φ –Η―Ö –Ϋ–Α –Ζ–Ϋ–Α–Κ–Η:
3. –£―΄–Ω–Η―¹―΄–≤–Α–Β–Φ ―Ä–Α–±–Ψ―΅―É―é ―¹―Ö–Β–Φ―É –Η ―Ä–Β―à–Α–Β–Φ –Ζ–Α–¥–Α―΅―É
–ü―Ä–Η ―Ä–Β―à–Β–Ϋ–Η–Η –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –±―É–Κ–≤–Β–Ϋ–Ϋ―΄–Β –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è
–≤ ―³–Ψ―Ä–Φ―É–Μ–Α―Ö (60) βÄî (63) –Ζ–Α–Φ–Β–Ϋ―è―é―² –Β–≥–Ψ ―ç–Μ–Β–Φ–Β–Ϋ―²–Α–Φ–Η.
–ü―Ä–Η –Η―¹―¹–Μ–Β–¥–Ψ–≤–Α–Ϋ–Η–Η ―³–Ψ―Ä–Φ―É–Μ –Ϋ–Α –Ζ–Ϋ–Α–Κ–Η –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Η–Φ–Β―²―¨ –≤ –≤–Η–¥―É
―¹–Μ–Β–¥―É―é―â–Β–Β:
―à–Η―Ä–Ψ―²–Α ―¹―Ä –≤―¹–Β–≥–¥–Α ―¹―΅–Η―²–Α–Β―²―¹―è –Ω–Ψ–Μ–Ψ–Ε–Η―²–Β–Μ―¨–Ϋ–Ψ–Ι;
―¹–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η–Β –±, –Β―¹–Μ–Η –Ϋ–Α–Η–Φ–Β–Ϋ–Ψ–≤–Α–Ϋ–Η–Β ―¹–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η―è –Ψ–¥–Ϋ–Ψ–Η–Φ–Β–Ϋ–Ϋ–Ψ ―¹ ―à–Η―Ä–Ψ―²–Ψ–Ι, ―¹―΅–Η―²–Α–Β―²―¹―è –Ω–Ψ–Μ–Ψ–Ε–Η―²–Β–Μ―¨–Ϋ―΄–Φ; –≤ –Ω―Ä–Ψ―²–Η–≤–Ϋ–Ψ–Φ ―¹–Μ―É―΅–Α–Β βÄî –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ―¨–Ϋ―΄–Φ;
–≤―΄―¹–Ψ―²–Α h –≤―¹–Β–≥–¥–Α –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Α –Ζ–Ϋ–Α–Κ–Ψ–Φ;
–Α–Ζ–Η–Φ―É―² –ê –≤ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –≤―¹–Β–≥–¥–Α ―Ä–Α―¹―¹–Φ–Α―²―Ä–Η–≤–Α–Β―²―¹―è
–Ω–Ψ–Μ―É–Κ―Ä―É–≥–Ψ–≤–Ψ–Ι. –ï―¹–Μ–Η –Α–Ζ–Η–Φ―É―² ―¹–≤–Β―²–Η–Μ–Α –¥–Α–Ϋ –≤ –Κ―Ä―É–≥–Ψ–≤–Ψ–Φ –Η–Μ–Η ―΅–Β―²–≤–Β―Ä―²–Κ–Ψ–Φ ―¹―΅–Β―²–Β, –Β–≥–Ψ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Ω–Β―Ä–Β–≤–Β―¹―²–Η –≤ –Ω–Ψ–Μ―É–Κ―Ä―É–≥–Ψ–≤–Ψ–Ι, –Α –Ζ–Α―²–Β–Φ –Η―¹―¹–Μ–Β–¥–Ψ–≤–Α―²―¨ ―³–Ψ―Ä–Φ―É–Μ―É –Ϋ–Α –Ζ–Ϋ–Α–Κ–Η. –ü―Ä–Η –Η―¹―¹–Μ–Β–¥–Ψ–≤–Α–Ϋ–Η–Η ―²―Ä–Η–≥–Ψ–Ϋ–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Η―Ö ―³―É–Ϋ–Κ―Ü–Η–Ι –Ϋ–Α –Ζ–Ϋ–Α–Κ–Η –Η–Φ–Β–Β―² –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –≤–Β–Μ–Η―΅–Η–Ϋ–Α –Ω–Ψ–Μ―É–Κ―Ä―É–≥–Ψ–≤–Ψ–≥–Ψ
–Α–Ζ–Η–Φ―É―²–Α;
―΅–Α―¹–Ψ–≤–Ψ–Ι ―É–≥–Ψ–Μ t ―Ä–Α―¹―¹–Φ–Α―²―Ä–Η–≤–Α–Β―²―¹―è ―²–Ψ–Μ―¨–Κ–Ψ –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Η–Ι (–Ψ–Ϋ –≤―¹–Β–≥–¥–Α –Φ–Β–Ϋ―¨―à–Β 180¬Α). –½–Ϋ–Α–Κ ―²―Ä–Η–≥–Ψ–Ϋ–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Η―Ö ―³―É–Ϋ–Κ―Ü–Η–Ι –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―²―¹―è
–≤–Β–Μ–Η―΅–Η–Ϋ–Ψ–Ι ―΅–Α―¹–Ψ–≤–Ψ–≥–Ψ ―É–≥–Μ–Α.
–ü―Ä–Η–Φ–Β―Ä 34. –î–Α–Ϋ–Ψ c―Ä = 56¬Α17',2N; 5 = 2¬Α40',4S –Η t = 18¬Α00 ,9 Ost.
–ù–Α–Ι―²–Η h –Η –ê.
–†–Β―à–Β–Ϋ–Η–Β. 1. –ü–Ψ–Μ―¨–Ζ―É―è―¹―¨ –Ω–Ψ–Μ―è―Ä–Ϋ―΄–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–Φ, –≤―΄–Ω–Η―¹―΄–≤–Α–Β–Φ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ―΄–Β
―³–Ψ―Ä–Φ―É–Μ―΄ (―Ä–Η―¹. 78);
cos (90¬ΑβÄîh) = cos (90¬ΑβÄîc―Ä) βÄΔ cos (90¬ΑβÄî–±) + sin (90¬ΑβÄî―¹p) βÄΔ sin (90¬ΑβÄî–±) βÄΔ cos t;
sin h = sin ―¹p βÄΔ sin –± + cos ―¹―Ä βÄΔ cos –± βÄΔ cos t ;
ctg A βÄΔ sin t = ctg (90¬ΑβÄî–±) βÄΔ sin (90¬ΑβÄî ―¹―Ä) βÄî cos (90¬ΑβÄî―¹―Ä) βÄΔ cos t;
ctg A βÄΔ sin t = t g –± βÄΔ cos ―¹―Ä βÄî sin ―¹―Ä βÄΔ cos t.
2. –£―΄–Ω–Η―¹―΄–≤–Α–Β–Φ ―Ä–Α–±–Ψ―΅–Η–Β ―³–Ψ―Ä–Φ―É–Μ―΄ –Η –Α–Ϋ–Α–Μ–Η–Ζ–Η―Ä―É–Β–Φ –Η―Ö –Ϋ–Α –Ζ–Ϋ–Α–Κ–Η:
–†–Η―¹. 77.

–†–Η―¹. 78.
3. –†–Β―à–Α–Β–Φ –Ζ–Α–¥–Α―΅―É –Ω–Ψ ―Ä–Α–±–Ψ―΅–Β–Ι ―¹―Ö–Β–Φ–Β.
–£ ―¹–≤―è–Ζ–Η ―¹ ―²–Β–Φ ―΅―²–Ψ –≤ ―Ä–Α―¹―¹–Φ–Α―²―Ä–Η–≤–Α–Β–Φ–Ψ–Φ –Ω―Ä–Η–Φ–Β―Ä–Β –Ψ–±–Α ―΅–Μ–Β–Ϋ–Α –Ω―Ä–Α–≤–Ψ–Ι ―΅–Α―¹―²–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è ctg –ê –Ψ–Κ–Α–Ζ–Α–Μ–Η―¹―¨ –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η, –≤ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Η –Ζ–Ϋ–Α–Κ–Η –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ―΄ –Ϋ–Α –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄–Β. –£ –Μ–Β–≤–Ψ–Ι ―΅–Α―¹―²–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –≤–Φ–Β―¹―²–Ψ lg (βÄîctg A) –≤―΄―΅–Η―¹–Μ–Β–Ϋ–Ψ lg ctg (180¬ΑβÄî–ê).
–£―΄―΅–Η―¹–Μ–Β–Ϋ–Ϋ―΄–Ι –Α–Ζ–Η–Φ―É―² –ê –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β ctg –ê –±―É–¥–Β―² –≤―¹–Β–≥–¥–Α –≤―΄―Ä–Α–Ε–Β–Ϋ –≤ –Ω–Ψ–Μ―É–Κ―Ä―É–≥–Ψ–≤–Ψ–Φ ―¹―΅–Β―²–Β. –Δ–Α–Κ –Κ–Α–Κ –Α–Ζ–Η–Φ―É―² –≤ –Ω–Ψ–Μ―É–Κ―Ä―É–≥–Ψ–≤–Ψ–Φ ―¹―΅–Β―²–Β
–Ψ―²―¹―΅–Η―²―΄–≤–Α–Β―²―¹―è –Ψ―² –Ω–Ψ–Μ―É–Ϋ–Ψ―΅–Ϋ–Ψ–Ι ―΅–Α―¹―²–Η –Φ–Β―Ä–Η–¥–Η–Α–Ϋ–Α –Ϋ–Α–±–Μ―é–¥–Α―²–Β–Μ―è (–Κ–Ψ―²–Ψ―Ä–Α―è –Ψ–¥–Ϋ–Ψ–Η–Φ–Β–Ϋ–Ϋ–Α ―¹ –Ω–Ψ–≤―΄―à–Β–Ϋ–Ϋ―΄–Φ –Ω–Ψ–Μ―é―¹–Ψ–Φ), ―²–Ψ –Ϋ–Α–Η–Φ–Β–Ϋ–Ψ–≤–Α–Ϋ–Η–Β
–Ω–Β―Ä–≤–Ψ–Ι –±―É–Κ–≤―΄ –≤―΄―΅–Η―¹–Μ–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Α–Ζ–Η–Φ―É―²–Α –≤―¹–Β–≥–¥–Α –Ψ–¥–Ϋ–Ψ–Η–Φ–Β–Ϋ–Ϋ–Ψ ―¹ –≥–Β–Ψ–≥―Ä–Α―³–Η―΅–Β―¹–Κ–Ψ–Ι ―à–Η―Ä–Ψ―²–Ψ–Ι. –ù–Α–Η–Φ–Β–Ϋ–Ψ–≤–Α–Ϋ–Η–Β –≤―²–Ψ―Ä–Ψ–Ι –±―É–Κ–≤―΄ –Α–Ζ–Η–Φ―É―²–Α –≤―¹–Β–≥–¥–Α
–Ψ–¥–Ϋ–Ψ–Η–Φ–Β–Ϋ–Ϋ–Ψ ―¹ –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Η–Φ ―΅–Α―¹–Ψ–≤―΄–Φ ―É–≥–Μ–Ψ–Φ.
–ü―Ä–Η–±–Μ–Η–Ε–Β–Ϋ–Ϋ–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β (–Η–Μ–Η –Κ–Ψ–Ϋ―²―Ä–Ψ–Μ―¨ ―ç―²–Ψ–Ι –Ζ–Α–¥–Α―΅–Η) –Φ–Ψ–Ε–Β―²
–±―΄―²―¨ –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Ψ ―¹ –Ω–Ψ–Φ–Ψ―â―¨―é –≥―Ä–Α―³–Η―΅–Β―¹–Κ–Ψ–≥–Ψ –Ω–Ψ―¹―²―Ä–Ψ–Β–Ϋ–Η―è –Ϋ–Β–±–Β―¹–Ϋ–Ψ–Ι
―¹―³–Β―Ä―΄ –≤ –Ζ–Α–¥–Α–Ϋ–Ϋ–Ψ–Ι ―à–Η―Ä–Ψ―²–Β. –ù–Α –Ϋ–Β–±–Β―¹–Ϋ–Ψ–Ι ―¹―³–Β―Ä–Β –Ω–Ψ –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Φ –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Α–Φ –Ϋ–Α–Ϋ–Ψ―¹―è―² ―¹–≤–Β―²–Η–Μ–Ψ, –Α –Ζ–Α―²–Β–Φ –Ψ–Ω―Ä–Β–¥–Β–Μ―è―é―² –Η―¹–Κ–Ψ–Φ―΄–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ (―Ä–Η―¹. 79). –î–Μ―è –Ϋ–Α―à–Β–≥–Ψ –Ω―Ä–Η–Φ–Β―Ä–Α h ~ 30¬Α –Η A~ N 160¬Α Ost.
–£–Ω–Β―Ä–Β–¥
–û–≥–Μ–Α–≤–Μ–Β–Ϋ–Η–Β
–ù–Α–Ζ–Α–¥
|
|
–™–Μ–Α–≤–Ϋ–Ψ–Β –Ζ–Α –Ϋ–Β–¥–Β–Μ―é
|
 –£–Α–Ε–Ϋ–Ψ–Β
–£–Α–Ε–Ϋ–Ψ–Β
 –£–Α–Ε–Ϋ–Ψ–Β
–£–Α–Ε–Ϋ–Ψ–Β
 –£–Α–Ε–Ϋ–Ψ–Β
–£–Α–Ε–Ϋ–Ψ–Β
 –£–Α–Ε–Ϋ–Ψ–Β
–£–Α–Ε–Ϋ–Ψ–Β
 –£–Α–Ε–Ϋ–Ψ–Β
–£–Α–Ε–Ϋ–Ψ–Β