–Ď–į–Ĺ–Ĺ–Ķ—Ä

–ö–į–ļ –Ņ–ĺ–ī–≥–ĺ—ā–ĺ–≤–ł—ā—Ć –ĺ–Ņ–Ķ—Ä–į—ā–ĺ—Ä–į –ī—Ä–ĺ–Ĺ–ĺ–≤ –∑–į 20 —á–į—Ā–ĺ–≤
|
¬ß 29. –ü–ĺ–Ĺ—Ź—ā–ł–Ķ –ĺ–Ī –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź—Ö –ł
–Ľ–ł–Ĺ–ł—Ź—Ö –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź
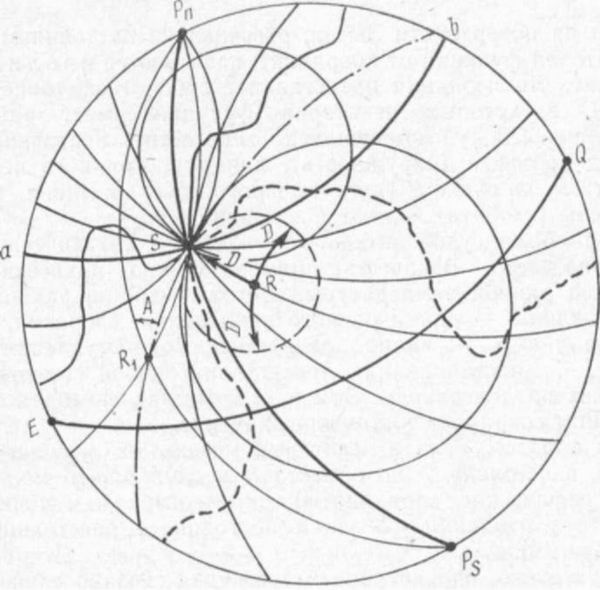
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –ľ–Ķ—Ā—ā–ĺ —Ā—É–ī–Ĺ–į –≤ –ľ–ĺ—Ä–Ķ ‚ÄĒ –∑–Ĺ–į—á–ł—ā –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –Ķ–≥–ĺ –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –≤ –ļ–į–ļ–ĺ–Ļ-—ā–ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā. –≠—ā–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—É—é —ā–ĺ—á–ļ—É 5 (—Ä–ł—Ā. 36), –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –≤ –ī–į–Ĺ–Ĺ–ĺ–Ķ –≤—Ä–Ķ–ľ—Ź –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź —Ā—É–ī–Ĺ–ĺ. –≠—ā—É —ā–ĺ—á–ļ—É S –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ľ–Ķ—Ä–ł–ī–ł–į–Ĺ–į –Ĺ–į–Ī–Ľ—é–ī–į—ā–Ķ–Ľ—Ź
PnSPs –ł –Ķ–≥–ĺ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ł aSb.
–í –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ —ā–į –∂–Ķ —ā–ĺ—á–ļ–į S —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ—á–ļ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź
—Ü–Ķ–Ľ–ĺ–≥–ĺ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ļ—Ä–ł–≤—č—Ö –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł (—Ā–ľ. —Ä–ł—Ā. 36).
–ü–ĺ—ć—ā–ĺ–ľ—É –ī–Ľ—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–ł –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł
–ó–Ķ–ľ–Ľ–ł (—ā. –Ķ. –ī–Ľ—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —Ā—É–ī–Ĺ–į)
–ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ —É–ľ–Ķ—ā—Ć –Ĺ–į–Ĺ–Ķ—Ā—ā–ł –Ĺ–į –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł
(–≥–Ľ–ĺ–Ī—É—Ā –ł–Ľ–ł –ļ–į—Ä—ā—É) –ī–≤–Ķ –Ľ—é–Ī—č–Ķ –ļ—Ä–ł–≤—č–Ķ –ł–∑ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ļ—Ä–ł–≤—č—Ö S,
–í –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā–Ľ—É—á–į—Ź—Ö –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–ł—ā–į—é—ā –Ņ–ĺ–Ľ—É—á–į—ā—Ć –į–Ĺ–į–Ľ–ł—ā–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ—É—ā–Ķ–ľ. –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
–ī–≤—É—Ö –Ľ—é–Ī—č—Ö –ļ—Ä–ł–≤—č—Ö –ł–∑ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į S —Ä–Ķ—ą–į—é—ā —Ā–ĺ–≤–ľ–Ķ—Ā—ā–Ĺ–ĺ.
–ė–∑ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ —á–ł—Ā–Ľ–į –ļ—Ä–ł–≤—č—Ö —ć—ā–ĺ–≥–ĺ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ľ–ĺ–∂–Ĺ–ĺ
–≤—č–ī–Ķ–Ľ–ł—ā—Ć —ā–į–ļ–ł–Ķ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ĺ–Ī–Ľ–į–ī–į—é—ā –ĺ—Ā–ĺ–Ī—č–ľ –ĺ—ā–Ľ–ł—á–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ
—Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ ‚ÄĒ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ĺ–≤–į—ā—Ć —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į–ľ —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ļ, –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ļ.
–ü—É—Ā—ā—Ć, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ł–∑ —ā–ĺ—á–ļ–ł S –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ D –ī–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į R, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į –∑–Ķ–ľ–Ĺ–ĺ–Ļ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł (—Ā–ľ. —Ä–ł—Ā. 36). –Ę–ĺ–≥–ī–į –ł–∑ –≤—Ā–Ķ—Ö –ļ—Ä–ł–≤—č—Ö —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į S –ľ–ĺ–∂–Ĺ–ĺ –≤—č–ī–Ķ–Ľ–ł—ā—Ć —ā–į–ļ—É—é –ļ—Ä–ł–≤—É—é,
–ļ–į–∂–ī–į—Ź —ā–ĺ—á–ļ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ (–≤ —ā–ĺ–ľ —á–ł—Ā–Ľ–Ķ –ł —ā–ĺ—á–ļ–į S) —É–ī–į–Ľ–Ķ–Ĺ–į –ĺ—ā –ĺ–Ī—ä–Ķ–ļ—ā–į R –Ĺ–į –ĺ–ī–Ĺ–ĺ –ł —ā–ĺ –∂–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ D. –≠—ā–į –ļ—Ä–ł–≤–į—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ä–į–ī–ł—É—Ā–į D —Ā
—Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ R.
–†–ł—Ā. 36.
–í—Ā–Ķ –Ľ–Ķ–∂–į—Č–ł–Ķ –Ĺ–į —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —ā–ĺ—á–ļ–ł (–Ņ—É–Ĺ–ļ—ā–ł—Ä –Ĺ–į —Ä–ł—Ā. 36) –ł–ľ–Ķ—é—ā —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č φ –ł
λ. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ī–į–Ĺ–Ĺ–į—Ź –ļ—Ä–ł–≤–į—Ź (–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć) –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł
–ó–Ķ–ľ–Ľ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—É—é —Ą—É–Ĺ–ļ—Ü–ł—é –ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –ĺ—ā–≤–Ķ—á–į—é—Č—É—é –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č ‚ÄĒ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—é D.
–ü—É—Ā—ā—Ć —ā–į –∂–Ķ —ā–ĺ—á–ļ–į S —É—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ł–∑ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į R1
–Ņ–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É –ź. –Ę–ĺ–≥–ī–į –ł–∑ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ļ—Ä–ł–≤—č—Ö S –ľ–ĺ–∂–Ĺ–ĺ –≤—č–ī–Ķ–Ľ–ł—ā—Ć –ļ—Ä–ł–≤—É—é, –ļ–į–∂–ī–į—Ź —ā–ĺ—á–ļ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —É—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ł–∑ –ĺ–Ī—ä–Ķ–ļ—ā–į R1 –Ņ–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É –ź. –≠—ā–į –ļ—Ä–ł–≤–į—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā –°–ĺ–Ī–ĺ–Ļ –ī—É–≥—É –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į
(—ą—ā—Ä–ł—Ö-–Ņ—É–Ĺ–ļ—ā–ł—Ä –Ĺ–į —Ä–ł—Ā. 36), –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č—É—é —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É R1 –ł S –ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č—É—é –ľ–Ķ—Ä–ł–ī–ł–į–Ĺ —ā–ĺ—á–ļ–ł R1 –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ, —Ä–į–≤–Ĺ—č–ľ –ź. –í—Ā–Ķ –Ľ–Ķ–∂–į—Č–ł–Ķ –Ĺ–į —ć—ā–ĺ–Ļ –ī—É–≥–Ķ –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į —ā–ĺ—á–ļ–ł –ł–ľ–Ķ—é—ā —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č cp –ł X. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ī–į–Ĺ–Ĺ–į—Ź –ļ—Ä–ł–≤–į—Ź –Ĺ–į
–Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł —ā–į–ļ–∂–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—É—é —Ą—É–Ĺ–ļ—Ü–ł—é –ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –ĺ—ā–≤–Ķ—á–į—é—Č—É—é –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é
–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č ‚ÄĒ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É –ź.
–Ě–į–ļ–ĺ–Ĺ–Ķ—Ü, –Ķ—Ā–Ľ–ł –Ĺ–į —Ā—É–ī–Ĺ–Ķ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–į –≥–Ľ—É–Ī–ł–Ĺ–į, —ā–ĺ –ł–∑ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į
–ļ—Ä–ł–≤—č—Ö S –ľ–ĺ–∂–Ĺ–ĺ –≤—č–ī–Ķ–Ľ–ł—ā—Ć —ā–į–ļ—É—é –ļ—Ä–ł–≤—É—é, –ļ–į–∂–ī–į—Ź —ā–ĺ—á–ļ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ
–Ī—É–ī–Ķ—ā –Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –Ĺ–į –≥–Ľ—É–Ī–ł–Ĺ–Ķ, —Ä–į–≤–Ĺ–ĺ–Ļ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ. –Ę–į–ļ–į—Ź –ļ—Ä–ł–≤–į—Ź
–Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł (–ł–∑–ĺ–Ī–į—ā–į) –Ī—É–ī–Ķ—ā –≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—ā—Ć
–Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—É—é —Ą—É–Ĺ–ļ—Ü–ł—é –ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –ĺ—ā–≤–Ķ—á–į—é—Č—É—é –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č ‚ÄĒ –≥–Ľ—É–Ī–ł–Ĺ–Ķ (–Ņ—É–Ĺ–ļ—ā–ł—Ä–Ĺ–į—Ź –Ľ–ł–Ĺ–ł—Ź –Ĺ–į —Ä–ł—Ā.
36).
–õ–ł–Ĺ–ł–ł –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł, –ĺ—ā–≤–Ķ—á–į—é—Č–ł–Ķ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź–ľ–ł.
–≠—ā–ĺ –∑–Ĺ–į—á–ł—ā, —á—ā–ĺ –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ľ–Ķ—Ā—ā–ĺ —ā–ĺ—á–Ķ–ļ, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –ł–ľ–Ķ–Ķ—ā –ĺ–ī–Ĺ–ĺ –ł —ā–ĺ
–∂–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ. –Ę–į–ļ, —É–Ņ–ĺ–ľ–ł–Ĺ–į–≤—ą–į—Ź—Ā—Ź –≤—č—ą–Ķ –Ľ–ł–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ī–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į (–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć), –Ľ–ł–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į –ź
–ł–∑ –ĺ–Ī—ä–Ķ–ļ—ā–į R1 –Ĺ–į —Ā—É–ī–Ĺ–ĺ S (–ī—É–≥–į –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į) –ł –Ľ–ł–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–Ļ –≥–Ľ—É–Ī–ł–Ĺ—č (–ł–∑–ĺ–Ī–į—ā–į) —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź–ľ–ł.
–° –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź–ľ–ł —Ā—É–ī–ĺ–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć –≤—Ā—ā—Ä–Ķ—á–į–Ķ—ā—Ā—Ź –≤ –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–į–Ī–ĺ—ā–Ķ –ī–ĺ–≤–ĺ–Ľ—Ć–Ĺ–ĺ —á–į—Ā—ā–ĺ. –í –ļ–į—á–Ķ—Ā—ā–≤–Ķ –Ņ—Ä–ł–ľ–Ķ—Ä–į –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł–≤–Ķ—Ā—ā–ł –ł–∑–ĺ—ā–Ķ—Ä–ľ—č‚ÄĒ –Ľ–ł–Ĺ–ł–ł —Ä–į–≤–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č, –ł–∑–ĺ–≥–ĺ–Ĺ—č ‚ÄĒ –Ľ–ł–Ĺ–ł–ł —Ä–į–≤–Ĺ–ĺ–≥–ĺ —Ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź, –ł–∑–ĺ–ļ–Ľ–ł–Ĺ—č ‚ÄĒ –Ľ–ł–Ĺ–ł–ł —Ä–į–≤–Ĺ–ĺ–≥–ĺ –Ĺ–į–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź, –ł–∑–ĺ—Ä–į—Ö–ł–ł, –ł–Ľ–ł –ļ–ĺ-
—ā–ł–ī–į–Ľ—Ć–Ĺ—č–Ķ –Ľ–ł–Ĺ–ł–ł, ‚ÄĒ –Ľ–ł–Ĺ–ł–ł –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į—Ā—ā—É–Ņ–Ľ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ
–≤–ĺ–ī—č –ł —ā. –ī. –ö–į–∂–ī–į—Ź –ł–∑ –Ĺ–ł—Ö –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ķ
–ľ–Ķ—Ā—ā–ĺ —ā–ĺ—á–Ķ–ļ –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź
–ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —Ā–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ.
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ķ—Ā–Ľ–ł –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ļ –ľ–ĺ–ľ–Ķ–Ĺ—ā –Ĺ–į —Ā—É–ī–Ĺ–Ķ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ—č,
–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ D –ī–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į R –ł –≥–Ľ—É–Ī–ł–Ĺ–į, —ā–ĺ –ľ–Ķ—Ā—ā–ĺ —Ā—É–ī–Ĺ–į
(–Ķ–≥–ĺ –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č) –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ā—Ź –ļ–į–ļ —ā–ĺ—á–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ī–≤—É—Ö –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ļ ‚ÄĒ –Ľ–ł–Ĺ–ł–ł –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź D –ī–ĺ
–ĺ–Ī—ä–Ķ–ļ—ā–į R –ł –ł–∑–ĺ–Ī–į—ā—č.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į —Ā–≤—Ź–∑–į–Ĺ–ĺ —Ā —Ä–į–∑–Ľ–ł—á–Ĺ–ĺ–≥–ĺ
—Ä–ĺ–ī–į –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł—Ź–ľ–ł, –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź–ľ–ł. –í—Ā—Ź–ļ–ĺ–Ķ –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ķ, –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ķ
–ī–į–Ķ—ā –ł–∑–ĺ–Ľ–ł–Ĺ–ł—é –ļ–į–ļ–ĺ–≥–ĺ-–Ľ–ł–Ī–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤–ł–ī–į. –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –≤—č–ī–Ķ–Ľ–ł—ā—Ć –ł–∑ –ĺ–Ī—Č–Ķ–≥–ĺ —á–ł—Ā–Ľ–į —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ļ—Ä–ł–≤—č—Ö –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č—É—é —á–Ķ—Ä–Ķ–∑ –ī–į–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł –≤–Ņ–ĺ–Ľ–Ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ—É—é –ļ—Ä–ł–≤—É—é ‚ÄĒ –ł–∑–ĺ–Ľ–ł–Ĺ–ł—é, –ĺ—ā–≤–Ķ—á–į—é—Č—É—é —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į–ľ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł—Ź. –ü–ĺ—Ā–Ľ–Ķ —ć—ā–ĺ–≥–ĺ –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź —ā–Ķ–ľ –ł–Ľ–ł –ł–Ĺ—č–ľ –Ņ—Ä–ł–Ķ–ľ–ĺ–ľ, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ—č–ľ –Ĺ–ł–∂–Ķ, –Ĺ–į–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –Ĺ–į –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł
–ó–Ķ–ľ–Ľ–ł ‚ÄĒ –≥–Ľ–ĺ–Ī—É—Ā –ł–Ľ–ł –ļ–į—Ä—ā—É. –Ę–ĺ—á–ļ–į, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–į—Ź –ĺ—ā –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź
–ī–≤—É—Ö –ł–Ľ–ł –Ī–ĺ–Ľ–Ķ–Ķ –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ļ, –ļ–į–∂–ī–į—Ź –ł–∑ –ļ–ĺ—ā–ĺ—Ä—č—Ö –ĺ—ā–≤–Ķ—á–į–Ķ—ā –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ –ī–Ľ—Ź –ĺ–Ī—Ā–Ķ—Ä–≤–į—Ü–ł–ł, –ī–į—Ā—ā –ľ–Ķ—Ā—ā–ĺ
—Ā—É–ī–Ĺ–į.
–í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā —Ö–į—Ä–į–ļ—ā–Ķ—Ä–į –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ļ –ł–∑–ĺ–Ľ–ł–Ĺ–ł–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –Ľ–ł–Ĺ–ł–ł. –Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł–∑ –Ĺ–ł—Ö
–ł–ľ–Ķ—é—ā –ī–ĺ–≤–ĺ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ļ –≤–ł–ī –ł –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ī–Ķ–∑ –ĺ—Ā–ĺ–Ī–ĺ–≥–ĺ —ā—Ä—É–ī–į –Ĺ–į–Ĺ–Ķ—Ā–Ķ–Ĺ—č –Ĺ–į –ļ–į—Ä—ā—É —Ā—É–ī–ĺ–≤–ĺ–ī–ł—ā–Ķ–Ľ–Ķ–ľ –≤ —ą—ā—É—Ä–ľ–į–Ĺ—Ā–ļ–ĺ–Ļ —Ä—É–Ī–ļ–Ķ. –Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ
–∂–Ķ –ł–∑–ĺ–Ľ–ł–Ĺ–ł–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ —Ā–Ľ–ĺ–∂–Ĺ—č–Ķ –ļ—Ä–ł–≤—č–Ķ, –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ
–ļ–ĺ—ā–ĺ—Ä—č—Ö –≤ —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –Ņ–Ľ–į–≤–į–Ĺ–ł—Ź –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –∑–į—ā—Ä—É–ī–Ĺ–Ķ–Ĺ–ĺ, –į –ł–Ĺ–ĺ–≥–ī–į
–Ņ—Ä–ĺ—Ā—ā–ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ. –í —ā–į–ļ–ł—Ö —Ā–Ľ—É—á–į—Ź—Ö –Ī–ĺ–Ľ—Ć—ą—É—é –Ņ–ĺ–ľ–ĺ—Č—Ć —Ā—É–ī–ĺ–≤–ĺ–ī–ł—ā–Ķ–Ľ—é –ĺ–ļ–į–∑—č–≤–į—é—ā —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ķ –ļ–į—Ä—ā—č –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ļ, –ĺ –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ņ–ĺ–ī—Ä–ĺ–Ī–Ĺ–Ķ–Ķ –Ī—É–ī–Ķ—ā —Ā–ļ–į–∑–į–Ĺ–ĺ –Ĺ–ł–∂–Ķ.
–ü—Ä–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź—Ö –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į–ľ–ł –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ļ –ł
–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ļ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ĺ–Ī—č—á–Ĺ–ĺ —É–≥–Ľ—č, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –Ľ–ł–Ī–ĺ —Ä–į–∑–Ĺ–ĺ—Ā—ā–ł
—Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ.
–†–ł—Ā. 37.
–†–ł—Ā. 38.
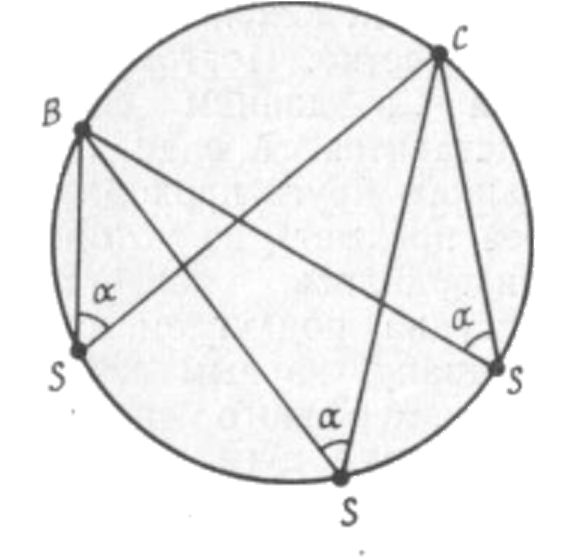
–ü—Ä–ł –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–ł —Ā —Ā—É–ī–Ĺ–į –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į –į –ľ–Ķ–∂–ī—É –ī–≤—É–ľ—Ź
–Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į–ľ–ł –í –ł –° —Ā—É–ī–Ĺ–ĺ –Ī—É–ī–Ķ—ā –Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł (—Ä–ł—Ā.
37), –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —ć—ā–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā—č, –Ņ—Ä–ł—á–Ķ–ľ –≤–Ķ—Ä—ą–ł–Ĺ–į S –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į –į –Ī—É–ī–Ķ—ā —ā–į–ļ–∂–Ķ –Ľ–Ķ–∂–į—ā—Ć –Ĺ–į —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–ü–Ķ–Ľ–Ķ–Ĺ–≥ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ —á–į—Ā—ā–Ĺ—č–Ļ —Ā–Ľ—É—á–į–Ļ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ
—É—ā–Ľ–į –ľ–Ķ–∂–ī—É –ī–≤—É–ľ—Ź –ĺ–Ī—ä–Ķ–ļ—ā–į–ľ–ł, –ĺ–ī–Ĺ–ł–ľ –ł–∑ –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ—é—Ā
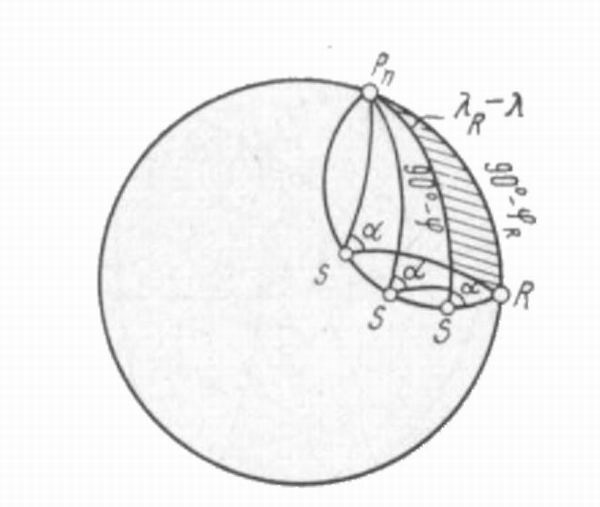
–ó–Ķ–ľ–Ľ–ł. –ē—Ā–Ľ–ł –Ņ–Ķ–Ľ–Ķ–Ĺ–≥ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į R (—Ä–ł—Ā. 38) —Ā –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ —Ā —Ā—É–ī–Ĺ–į, –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —ā–ĺ –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā—Ā—Ź –Ī–Ľ–ł–∑–ļ–ĺ–Ļ –ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ļ—Ä–ł–≤–ĺ–Ļ –Ľ–ł–Ĺ–ł–Ķ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ –Ņ–ĺ–Ľ—é—Ā –ó–Ķ–ľ–Ľ–ł –†–Ņ –ł –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É–Ķ–ľ—č–Ļ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā R.
–≠—ā–į –Ľ–ł–Ĺ–ł—Ź ‚ÄĒ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ľ–Ķ—Ā—ā–ĺ –≤–Ķ—Ä—ą–ł–Ĺ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —É–≥–Ľ–į
PnSR –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, —Ä–į–≤–Ĺ–ĺ–Ļ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–ľ—É –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É, —ā. –Ķ.
–Ľ–ł–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į, –ł –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ł–∑–ĺ–Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–Ļ, –ł–Ľ–ł
–ł–∑–ĺ–į–∑–ł–ľ—É—ā–ĺ–Ļ.
–ė–∑ –Ľ—é–Ī–ĺ–Ļ —ā–ĺ—á–ļ–ł S –ł–∑–ĺ–į–∑–ł–ľ—É—ā—č (—Ā–ľ. —Ä–ł—Ā. 38) –Ņ–Ķ–Ľ–Ķ–Ĺ–≥ –Ĺ–į –ĺ–Ī—ä–Ķ–ļ—ā
R –ĺ–ī–ł–Ĺ –ł —ā–ĺ—ā –∂–Ķ –į.
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ľ–ł–Ĺ–ł–ł —Ä–į–≤–Ĺ—č—Ö –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤ –Ľ–Ķ–≥–ļ–ĺ –≤—č–≤–Ķ—Ā—ā–ł, —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—Ź –Ľ—é–Ī–ĺ–Ļ –ł–∑ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ –†‚Äě RS, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ—č PnR = 90¬į ‚ÄĒ φ–Ľ ; P n S = (90¬į - φ) , —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —É–≥–Ľ—č RPn S = (λR - λ),
PnSR = –į.
–ü—Ä–ł–ľ–Ķ–Ĺ—Ź—Ź –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—É—é —Ą–ĺ—Ä–ľ—É–Ľ—É —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł–ł, —Ā–≤—Ź–∑—č–≤–į—é—Č—É—é —á–Ķ—ā—č—Ä–Ķ —Ä—Ź–ī–ĺ–ľ –Ľ–Ķ–∂–į—Č–ł—Ö —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į, —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ł–∑–ĺ–į–∑–ł–ľ—É—ā—č –Ņ–ĺ–Ľ—É—á–į—é—ā –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ –≤–ł–ī–Ķ:
–≥–ī–Ķ –į, φR λR ‚ÄĒ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ—č–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, —ā. –Ķ. –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č –Ľ–ł–Ĺ–ł–ł —Ä–į–≤–Ĺ—č—Ö
–Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤;
φ , λ ‚ÄĒ –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ—č–Ķ (–ł—Ā–ļ–ĺ–ľ—č–Ķ) –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į S (—ā–Ķ–ļ—É—Č–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č).
–í –ľ–ĺ—Ä—Ā–ļ–ĺ–Ļ –Ņ—Ä–į–ļ—ā–ł–ļ–Ķ –ľ–Ķ—Ā—ā–ĺ —Ā—É–ī–Ĺ–į –ľ–ĺ–∂–Ķ—ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—ā—Ć—Ā—Ź –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤–į–Ĺ–ł–Ķ–ľ –Ķ–≥–ĺ —Ā –Ī–Ķ—Ä–Ķ–≥–į –ł–Ľ–ł —Ā –ī—Ä—É–≥–ĺ–≥–ĺ —Ā—É–ī–Ĺ–į. –í —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥
—Ā—É–ī–Ĺ–į, –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ
S (—Ä–ł—Ā. 39) –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł
–ó–Ķ–ľ–Ľ–ł –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, –ł–∑–ľ–Ķ—Ä—Ź—é—ā
–ł–∑ —ā–ĺ—á–ļ–ł, –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ R –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ. –ü–ĺ—ć—ā–ĺ–ľ—É –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź –≤ –ī–į–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā—Ā—Ź –≤ –≤–ł–ī–Ķ –ī—É–≥–ł
–Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ
—á–Ķ—Ä–Ķ–∑ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā, –ł–∑ –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł–Ľ–ĺ—Ā—Ć –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤–į–Ĺ–ł–Ķ —Ā—É–ī–Ĺ–į, –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ –ļ –Ķ–≥–ĺ
–ľ–Ķ—Ä–ł–ī–ł–į–Ĺ—É, —Ä–į–≤–Ĺ—č–ľ –≤–Ķ–Ľ–ł—á–ł–Ĺ–Ķ –ź –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į.

–†–ł—Ā. 39.
–Ĺ–Ķ –ź –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į.
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ī—É–≥–ł –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ
–ļ—Ä—É–≥–į –ľ–ĺ–∂–Ĺ–ĺ –≤—č–≤–Ķ—Ā—ā–ł, —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—Ź –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł FSL
–ł RF H (—Ā–ľ. —Ä–ł—Ā. 39), –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö F ‚ÄĒ —ā–ĺ—á–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź
–ī—É–≥–ł –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į —Ā-—ć–ļ–≤–į—ā–ĺ—Ä–ĺ–ľ; —Ā—ā–ĺ—Ä–ĺ–Ĺ—č SL = φ ; FL = (λ ‚ÄĒ λ0);
RH = φ–ö; FH = (λR ‚ÄĒ λ0); —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —É–≥–Ľ—č RF H = 90¬į ‚ÄĒ –ź;
FR H = –ź ‚ÄĒ 180¬į; SLF = RH F = 90¬į.
–ü—Ä–ł–ľ–Ķ–Ĺ—Ź—Ź –Ņ—Ä–į–≤–ł–Ľ–ĺ –ú–ĺ–ī—é–ł‚ÄĒ–Ě–Ķ–Ņ–Ķ—Ä–į, –Ņ–ĺ–Ľ—É—á–ł–ľ –ī–Ľ—Ź –ī—É–≥–ł –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į —Ā–Ľ–Ķ–ī—É—é—Č—É—é –≥—Ä—É–Ņ–Ņ—É —Ą–ĺ—Ä–ľ—É–Ľ:
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ņ—Ä–ł –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤–į–Ĺ–ł–ł –Ī–Ķ—Ä–Ķ–≥–ĺ–≤–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į —Ā —Ā—É–ī–Ĺ–į –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ķ–Ļ –Ī—É–ī–Ķ—ā –Ľ–ł–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č—Ö –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤.
–ü—Ä–ł –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–ł –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į —Ā—É–ī–Ĺ–į —Ā –Ī–Ķ—Ä–Ķ–≥–į –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī—É–≥–ĺ–Ļ –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–Ĺ—č–Ķ —Ā–Ľ—É—á–į–ł —Ā –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–ĺ—á–ļ–ł –∑—Ä–Ķ–Ĺ–ł—Ź —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ—č, –ĺ–Ī —ć—ā–ĺ–ľ —Ā–Ľ–Ķ–ī—É–Ķ—ā –Ņ–ĺ–ľ–Ĺ–ł—ā—Ć –Ņ—Ä–ł –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–į–Ī–ĺ—ā–Ķ –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į –≤ –ľ–ĺ—Ä–Ķ.
–≥–ī–Ķ –ź, λ0, –ź, φR, λR - –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č (–ź0 –ł λ0 -–ļ—É—Ä —Ā –ł –ī–ĺ–Ľ–≥–ĺ—ā–į –Ņ—Ä–ł
–Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł–ł –ī—É–≥–ĺ–Ļ –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į —ć–ļ–≤–į—ā–ĺ—Ä–į),
φ –ł λ ‚ÄĒ —ā–Ķ–ļ—É—Č–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į.
–ü—Ä–ł –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ī–ĺ –Ī–Ķ—Ä–Ķ–≥–ĺ–≤–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į —Ā —Ā—É–ī–Ĺ–į
–ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ķ–Ļ –Ī—É–ī–Ķ—ā —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–į—Ź –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł,
–ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–į—Ź –ł–∑ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ĺ–Ī—ä–Ķ–ļ—ā–į R, –ļ–į–ļ –ł–∑ –Ņ–ĺ–Ľ—é—Ā–į, —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ
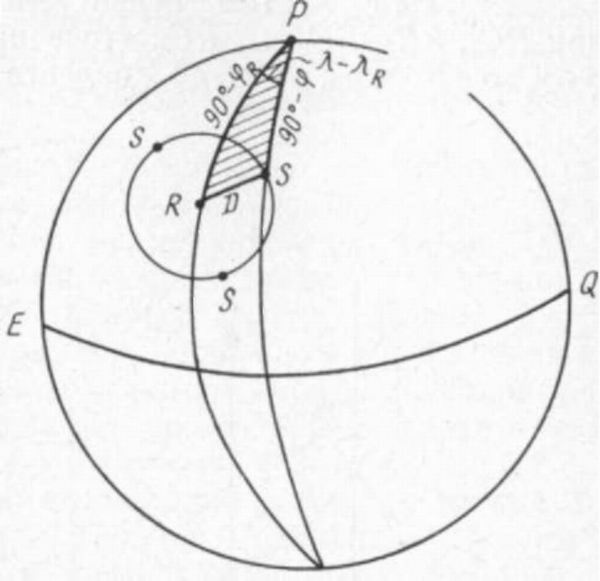
—Ä–į–ī–ł—É—Ā–ĺ–ľ, —Ä–į–≤–Ĺ—č–ľ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–Ĺ–ĺ–ľ—É —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—é D (—Ä–ł—Ā. 40).
–†–ł—Ā. 40.
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ
–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ľ–ĺ–∂–Ĺ–ĺ –≤—č–≤–Ķ—Ā—ā–ł,
—Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—Ź —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ļ
—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ PRS (–Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ
–∑–į—ą—ā—Ä–ł—Ö–ĺ–≤–į–Ĺ), –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ PR = 90¬į ‚ÄĒ φR; PS = 90¬į‚ÄĒφ; RS = D ‚ÄĒ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ņ–ĺ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł –ľ–Ķ–∂–ī—É —Ā—É–ī–Ĺ–ĺ–ľ –ł
–Ī–Ķ—Ä–Ķ–≥–ĺ–≤—č–ľ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–ľ; RPS ‚ÄĒ
—Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ļ —É–≥–ĺ–Ľ, —Ä–į–≤–Ĺ—č–Ļ
(λ ‚ÄĒ –õλ).
–ü—Ä–ł–ľ–Ķ–Ĺ—Ź—Ź –Ņ–Ķ—Ä–≤—É—é –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—É—é —Ą–ĺ—Ä–ľ—É–Ľ—É —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł–ł, —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–Ľ—É—á–į—é—ā
–≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ –≤–ł–ī–Ķ:
–≥–ī–Ķ D, φR , λR ‚ÄĒ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł;
φ, λ ‚ÄĒ —ā–Ķ–ļ—É—Č–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į.
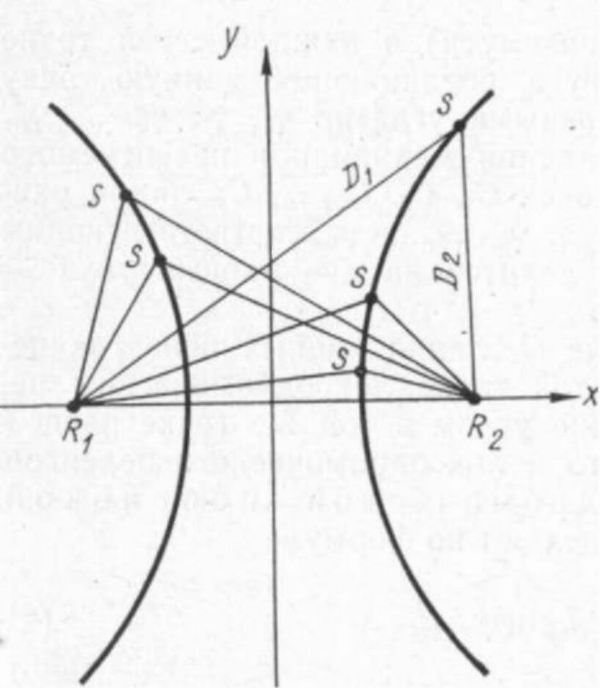
–†–ł—Ā. 41.
–í —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö
–ī–į–Ľ—Ć–Ĺ–Ķ–Ļ —Ä–į–ī–ł–ĺ–Ĺ–į–≤–ł–≥–į—Ü–ł–ł –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź—é—ā –ľ–Ķ—ā–ĺ–ī –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź —Ā —Ā—É–ī–Ĺ–į –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ļ –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł —Ä–į–∑–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź AD –ī–ĺ
–ī–≤—É—Ö —Ä–į–ī–ł–ĺ—Ā—ā–į–Ĺ—Ü–ł–Ļ (–ł–ľ–Ņ—É–Ľ—Ć—Ā–Ĺ—č–Ķ –ł —Ą–į–∑–ĺ–≤—č–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č). –í
—ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –ł–∑–ĺ–Ľ–ł–Ĺ–ł—Ź –ł–∑–ĺ–Ī—Ä–į–∑–ł—ā—Ā—Ź –≤ –≤–ł–ī–Ķ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ó–Ķ–ľ–Ľ–ł, —Ą–ĺ–ļ—É—Ā—č –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ R1 –ł R2 (—Ä–ł—Ā. 41) —Ā–ĺ–≤–Ņ–į–ī–į—é—ā —Ā –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź–ľ–ł —É–Ņ–ĺ–ľ—Ź–Ĺ—É—ā—č—Ö
—Ä–į–ī–ł–ĺ—Ā—ā–į–Ĺ—Ü–ł–Ļ.
–Ě–į –ľ–Ķ—Ä–ļ–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ –ļ—Ä–ł–≤—č–Ķ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–Ĺ—č—Ö –≤—č—ą–Ķ –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ļ
(–ī—É–≥–ł –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į, –ł–∑–ĺ-
–į–∑–ł–ľ—É—ā—č, —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č) –≤—č–≥–Ľ—Ź–ī—Ź—ā
–ł–Ĺ–į—á–Ķ, —á–Ķ–ľ –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –∑–Ķ–ľ–Ĺ–ĺ–≥–ĺ —Ā—Ą–Ķ—Ä–ĺ–ł–ī–į.
–ö–į–ļ —É–ļ–į–∑—č–≤–į–Ľ–ĺ—Ā—Ć, –ī—É–≥–į –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į –Ĺ–į –ľ–Ķ—Ä–ļ–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ
–ł–ľ–Ķ–Ķ—ā –≤–ł–ī –ļ—Ä–ł–≤–ĺ–Ļ –Ľ–ł–Ĺ–ł–ł, –≤—č–≥–Ĺ—É—ā–ĺ–Ļ –≤ —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ī–Ľ–ł–∂–į–Ļ—ą–Ķ–≥–ĺ –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—é—Ā–į (—Ä–ł—Ā. 42), –ė–∑–ĺ–į–∑–ł–ľ—É—ā–į –∂–Ķ (–Ņ—Ä–ł –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ł—Ö
—Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö –ľ–Ķ–∂–ī—É —Ā—É–ī–Ĺ–ĺ–ľ –ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–ľ) –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–į
–ľ–Ķ–ļ—Ä–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ –ļ—Ä–ł–≤–ĺ–Ļ –Ľ–ł–Ĺ–ł–Ķ–Ļ, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –ī—É–≥–į–ľ –Ī–ĺ–Ľ—Ć—ą–ł—Ö –ļ—Ä—É–≥–ĺ–≤, –Ņ–ĺ –ī—Ä—É–≥—É—é —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –ĺ—ā –Ņ—Ä—Ź–ľ—č—Ö –Ľ–ł–Ĺ–ł–Ļ
RC1 RC2, RC3, RCn, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–ł—Ö –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ķ –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į –°1
–°2, –°3, –°n —Ā –ľ–Ķ—Ā—ā–ĺ–ľ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É–Ķ–ľ–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į R. –ü—Ä—Ź–ľ—č–Ķ –Ľ–ł–Ĺ–ł–ł RC1, RC2, RC3, RCn (—ā–ĺ—á–Ķ—á–Ĺ—č–Ļ –Ņ—É–Ĺ–ļ—ā–ł—Ä) –Ĺ–į–∑—č–≤–į—é—ā –Ľ–ł–Ĺ–ł—Ź–ľ–ł
–Ľ–ĺ–ļ—Ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į.

–†–ł—Ā. 42.
–õ–ł–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č—Ö –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤ (–ł–∑–ĺ–į–∑–ł–ľ—É—ā–į) –≤ –ļ–į–∂–ī–ĺ–Ļ —Ā–≤–ĺ–Ķ–Ļ —ā–ĺ—á–ļ–Ķ
–Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā—Ā—Ź –ī—É–≥–ĺ–Ļ –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–Ķ–Ļ –ī–į–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É
—Ā –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É–Ķ–ľ—č–ľ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–ľ –Ņ–ĺ–ī —Ä–į–∑–Ĺ—č–ľ–ł —É–≥–Ľ–į–ľ–ł: Y1, Y2, Y3.
–≠—ā–ł —É–≥–Ľ—č –Ĺ–į–∑—č–≤–į—é—ā —É–≥–Ľ–į–ľ–ł —Ā—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –ľ–Ķ—Ä–ł–ī–ł–į–Ĺ–ĺ–≤ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É–Ķ–ľ–ĺ–≥–ĺ
–Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į R –ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö —ā–ĺ—á–Ķ–ļ –°1, –°2, –°3, –°‚Äě –Ľ–ł–Ĺ–ł–ł —Ä–į–≤–Ĺ—č—Ö –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤. –ö–į–∂–ī—č–Ļ –ł–∑ —É–≥–Ľ–ĺ–≤ Y1, Y2, Y3,.... –£–Ņ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–ľ
–Ķ–ľ—É –Ľ–ĺ–ļ—Ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–ľ –ī–Ķ–Ľ–ł—ā—Ā—Ź –Ĺ–į –ī–≤–į —Ä–į–≤–Ĺ—č—Ö —É–≥–Ľ–į ‚ÄĒ
—É–≥–Ľ—č W1, W2, W3 ..., Wn.
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤ –Ľ—é–Ī–ĺ–Ļ —ā–ĺ—á–ļ–Ķ –°i –Ľ–ł–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č—Ö –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤ –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā—Ā—Ź —Ā —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–ľ —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–Ķ –Ľ–ĺ–ļ—Ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–ľ –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ Wi. –ü–ĺ–ī —ā–Ķ–ľ –∂–Ķ —É–≥–Ľ–ĺ–ľ –≤ —ā–ĺ–Ļ –∂–Ķ —ā–ĺ—á–ļ–Ķ –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –ł –Ľ–ł–Ĺ–ł–ł –ĺ—Ä—ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł –Ľ–ĺ–ļ—Ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤.
–£–≥–ĺ–Ľ W –Ĺ–į–∑—č–≤–į—é—ā –ĺ—Ä—ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ņ–ĺ–Ņ—Ä–į–≤–ļ–ĺ–Ļ.
–ē–≥–ĺ –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ
–≥–ī–Ķ –ź–õ, ‚ÄĒ —Ä–į–∑–Ĺ–ĺ—Ā—ā—Ć –ī–ĺ–Ľ–≥–ĺ—ā –ľ–Ķ–∂–ī—É –ľ–Ķ—Ā—ā–ĺ–ľ —Ā—É–ī–Ĺ–į –ł –Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É–Ķ–ľ—č–ľ
–Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–ľ, –į
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–į—Ź –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –Ĺ–į –ľ–Ķ—Ä–ļ–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ –ł–ľ–Ķ–Ķ—ā –≤–ł–ī
—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ļ—Ä–ł–≤–ĺ–Ļ, –Ī–Ľ–ł–∑–ļ–ĺ–Ļ –Ņ–ĺ —Ą–ĺ—Ä–ľ–Ķ –ļ —ć–Ľ–Ľ–ł–Ņ—Ā—É.
–†–į–Ī–ĺ—ā—É —ą—ā—É—Ä–ľ–į–Ĺ–į –Ņ–ĺ –Ņ—Ä–ĺ–ļ–Ľ–į–ī–ļ–Ķ –ļ—Ä–ł–≤—č—Ö –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ļ –Ĺ–į –ľ–Ķ—Ä–ļ–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ –ľ–ĺ–∂–Ĺ–ĺ –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —É–Ņ—Ä–ĺ—Ā—ā–ł—ā—Ć, –Ķ—Ā–Ľ–ł –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ĺ–Ļ —É—á–į—Ā—ā–ĺ–ļ –ļ—Ä–ł–≤–ĺ–Ļ –ł–∑–ĺ–Ľ–ł–Ĺ–ł–ł –∑–į–ľ–Ķ–Ĺ–ł—ā—Ć –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–ľ –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ļ –Ĺ–Ķ–Ļ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, —Ā–ĺ–≤–Ķ—Ä—ą–į—Ź –Ņ—Ä–ł —ć—ā–ĺ–ľ –ī–ĺ–Ņ—É—Ā—ā–ł–ľ—É—é –≤ –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –≤–ĺ–Ņ—Ä–ĺ—Ā–į—Ö –Ņ–ĺ–≥—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā—Ć. –Ę–į–ļ–ł–Ķ –≤—Ā–Ņ–ĺ–ľ–ĺ–≥–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ĺ—ā—Ä–Ķ–∑–ļ–ł –Ņ—Ä—Ź–ľ—č—Ö –Ľ–ł–Ĺ–ł–Ļ,
–∑–į–ľ–Ķ–Ĺ—Ź—é—Č–ł–Ķ –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ł–Ķ —É—á–į—Ā—ā–ļ–ł –ļ—Ä–ł–≤—č—Ö –ł–∑–ĺ–Ľ–ł–Ĺ–ł–Ļ, –Ĺ–į–∑—č–≤–į—é—ā –Ľ–ł–Ĺ–ł—Ź–ľ–ł –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź.
–ü—Ä–ł –≤–ł–∑—É–į–Ľ—Ć–Ĺ—č—Ö –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł—Ź—Ö —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ī–ĺ –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö
–ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤ —Ā–ĺ–≤—Ā–Ķ–ľ –Ĺ–Ķ–∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ—č. –≠—ā–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ķ—Č–Ķ –Ī–ĺ–Ľ–Ķ–Ķ —É–Ņ—Ä–ĺ—Ā—ā–ł—ā—Ć –Ņ—Ä–ĺ–ļ–Ľ–į–ī–ļ—É –Ľ–ł–Ĺ–ł–Ļ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ĺ–į –ľ–Ķ—Ä–ļ–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ. –Ę–į–ļ, –≤
—Ā–Ľ—É—á–į–Ķ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź –≤–ł–∑—É–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –Ľ–ł–Ĺ–ł—Ź –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ĺ–į
–ľ–Ķ—Ä–ļ–į—ā–ĺ—Ä—Ā–ļ–ĺ–Ļ –ļ–į—Ä—ā–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–į –ĺ–Ī—č—á–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć—é. –õ–ł–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č—Ö –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–ĺ–≤ –Ņ—Ä–ł –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –ī–ĺ
–Ņ–Ķ–Ľ–Ķ–Ĺ–≥—É–Ķ–ľ–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ľ–ł–Ĺ–ł–Ķ–Ļ –Ľ–ĺ–ļ—Ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į –ł –Ņ–ĺ—ć—ā–ĺ–ľ—É –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–į –Ĺ–į –ļ–į—Ä—ā–Ķ –≤ –≤–ł–ī–Ķ
–Ņ—Ä—Ź–ľ–ĺ–Ļ.
–ü—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź (–≤ –ľ–ł–Ľ—Ź—Ö), –Ņ—Ä–ł –ļ–ĺ—ā–ĺ—Ä—č—Ö –ľ–ĺ–∂–Ĺ–ĺ –Ī–Ķ–∑
—Ā—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö –Ņ–ĺ–≥—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā–Ķ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć –Ņ—Ä–ĺ–ļ–Ľ–į–ī–ļ—É –ł–∑–ĺ–į–∑–ł–ľ—É—ā—č
(–ł –ī—É–≥–ł –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ—Ä—É–≥–į) –≤ –≤–ł–ī–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ľ–ł–Ĺ–ł–ł –Ľ–ĺ–ļ—Ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ
–Ņ–Ķ–Ľ–Ķ–Ĺ–≥–į, —ā. –Ķ. –Ī–Ķ–∑ —É—á–Ķ—ā–į –ĺ—Ä—ā–ĺ–ī—Ä–ĺ–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ņ–ĺ–Ņ—Ä–į–≤–ļ–ł, –ī–į–Ĺ—č –≤ —ā–į–Ī–Ľ. 2.
–ö–į–∂–ī–ĺ–Ķ –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ķ –ī–į–Ķ—ā –ĺ–ī–Ĺ—É –Ľ–ł–Ĺ–ł—é –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź. –Ē–Ľ—Ź –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź –ĺ–Ī—Ā–Ķ—Ä–≤–ĺ–≤–į–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–Ķ—Ā—ā–į —Ā—É–ī–Ĺ–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ł–ľ–Ķ—ā—Ć –Ņ–ĺ –ļ—Ä–į–Ļ–Ĺ–Ķ–Ļ
–ľ–Ķ—Ä–Ķ –ī–≤–Ķ –Ľ–ł–Ĺ–ł–ł –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź: –ĺ–Ī—Ā–Ķ—Ä–≤–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ķ –ľ–Ķ—Ā—ā–ĺ —Ā—É–ī–Ĺ–į –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –ļ–į–ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź —ć—ā–ł—Ö –ī–≤—É—Ö –Ľ–ł–Ĺ–ł–Ļ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź.
–Ę–į–Ī–Ľ–ł—Ü–į 2
–í–Ņ–Ķ—Ä–Ķ–ī
–ě–≥–Ľ–į–≤–Ľ–Ķ–Ĺ–ł–Ķ
–Ě–į–∑–į–ī
|
|
–ď–Ľ–į–≤–Ĺ–ĺ–Ķ –∑–į –Ĺ–Ķ–ī–Ķ–Ľ—é
|
 –í–į–∂–Ĺ–ĺ–Ķ
–í–į–∂–Ĺ–ĺ–Ķ
 –í–į–∂–Ĺ–ĺ–Ķ
–í–į–∂–Ĺ–ĺ–Ķ
 –í–į–∂–Ĺ–ĺ–Ķ
–í–į–∂–Ĺ–ĺ–Ķ
 –í–į–∂–Ĺ–ĺ–Ķ
–í–į–∂–Ĺ–ĺ–Ķ
 –í–į–∂–Ĺ–ĺ–Ķ
–í–į–∂–Ĺ–ĺ–Ķ